8.4. Tipus de variables i SPSS
8.4.2. Codificació de les variables del fitxer d’exemples
Sexe: {1 = Home, 2 = Dona}
Tipus de centre: {1 = Públic, 2 = Privat}
Estudis que cursa: {1 = Primària – 1r. cicle d’ESO; 2 = 2n. cicle d’ESO – Batxillerat; 3 = Formació professional de grau mitjà}
Hàbitat: {1 = Rural, 2 = Urbà}
Estudis del pare: {1 = Sense estudis, 2 = Estudis primaris, 3 = Batxillerat o equivalents, 4 = Diplomat, llicenciat o equivalents}
Estudis de la mare: {1 = Sense estudis, 2 = Estudis primaris, 3 = Batxillerat o equivalents, 4 = Diplomat, llicenciat o equivalents}
Importància que es dona als diners: {1 = Molt poca, 2 = Poca, 3 = Mitjana, 4 = Molta, 5 = Moltíssima}
Publicitat: {1 = Cartells, 2 = Internet, 3 = Mòbil, 4 = RRSS, 5 = Televisió}
RRSS: {1 = Facebook, 2 = Instagram, 3 = Snapchat, 4 = TikTok, 5 = Twitter, 6 = WhatsApp, 7 = YouTube}
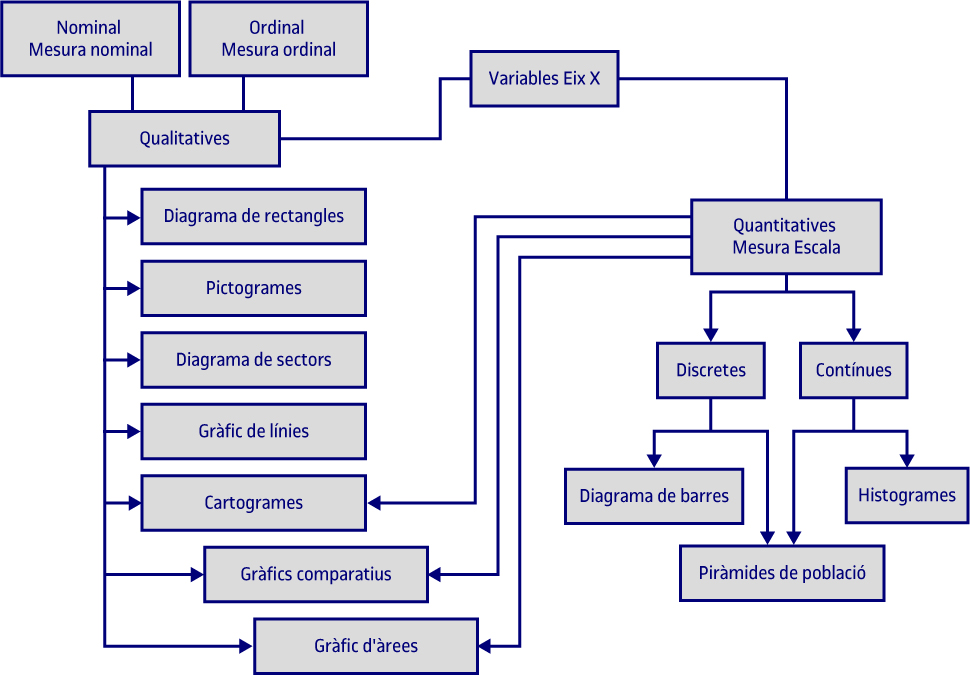
A l’hora de fer els gràfics de les variables dels dos fitxers (publicitat i RRSS), cal tenir en compte que, depenent del tipus de variable que aparegui en l’eix X, s’ha de fer un tipus de gràfic o un altre.
Per aprofundir
A continuació s’ha treballat amb les dades del fitxer publicitat i fent ús de l’SPSS (es poden fer els càlculs amb la seva versió gratuïta PSPP), es mostren les sortides del programa i les interpretacions de tots els resultats estadístics als quals s’ha fet referència de manera teòrica anteriorment.
En aquest cas la grandària de la mostra ha estat de 100 alumnes.
En la primera taula s’observen els valors dels estadístics de les variables qualitatives nominals del fitxer.
| Estadístics | |||||
| Sexe | Tipus de centre d’estudis | Hàbitat | Mitjà anuncis publicitaris codificat | ||
| N | Vàlid | 100 | 100 | 100 | 100 |
| Perduts | 0 | 0 | 0 | 0 | |
| Moda | 1a | 1 | 2 | 4 | |
Veiem que per a totes les variables la grandària de la mostra és de 100 i no hi ha valors perduts, i la moda de la variable Sexe no és única. En canvi, per al tipus de centre d’estudis, el valor de la variable que es repeteix més és l’1; és a dir, hi ha més centres públics que privats. L’hàbitat més repetit és el que pren el valor 2, és a dir, urbà, i el mitjà publicitari més repetit en les respostes dels enquestats és el que pren el valor 4en la codificació, és a dir, que els enquestats veuen més publicitat a les xarxes socials.
| Sexe | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Home | 50 | 50,0 | 50,0 | 50,0 |
| Dona | 50 | 50,0 | 50,0 | 100,0 | |
| Total | 100 | 100,0 | 100,0 | ||
Quant al sexe dels enquestats, el 50 % són homes i el 50 % són dones.
| Tipus de centre d’estudis | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Públic | 76 | 76,0 | 76,0 | 76,0 |
| Privat | 24 | 24,0 | 24,0 | 100,0 | |
| Total | 100 | 100,0 | 100,0 | ||
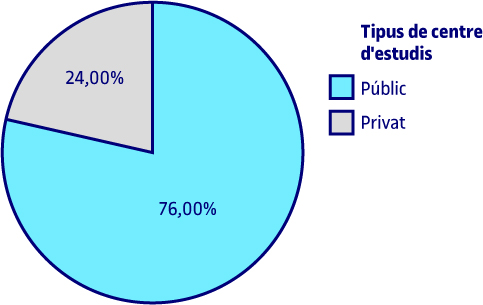
Anteriorment ja s’ha comentat que havien estat seleccionats més centres públics que privats, en concret, 76 centres públics i 24 centres privats. Com que la mostra és de grandària 100, la freqüència absoluta coincideix amb el percentatge. En no haver-hi dades perdudes, el percentatge per a cada tipus de centre d’estudis coincideix amb el percentatge vàlid.
| Hàbitat | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Rural | 46 | 46,0 | 46,0 | 46,0 |
| Urbà | 54 | 54,0 | 54,0 | 100,0 | |
| Total | 100 | 100,0 | 100,0 | ||
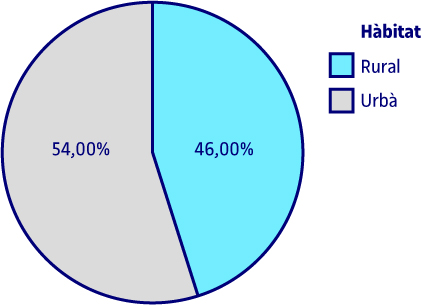
Pel que fa a l’hàbitat, la taula anterior ens indica que hi havia més centres urbans que rurals, en , 54 centres urbans i 46 rurals.
| Mitjà anuncis publicitaris codificat | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Cartells | 11 | 11,0 | 11,0 | 11,0 |
| Internet | 30 | 30,0 | 30,0 | 41,0 | |
| Mòbil | 20 | 20,0 | 20,0 | 61,0 | |
| RRSS | 31 | 31,0 | 31,0 | 92,0 | |
| Televisió | 8 | 8,0 | 8,0 | 100,0 | |
| Total | 100 | 100,0 | 100,0 | ||
Els mitjans assenyalats pels alumnes en els quals veuen majoritàriament anuncis publicitaris són cartells publicitaris, internet, mòbil, xarxes socials i televisió. S’observa que ningú no ha contestat que els vegin en la premsa o que els escoltin en la ràdio. L’11 % d’ells ha vist publicitat majoritàriament en cartells publicitaris, el 30 % a internet, el 20 % en el mòbil, el 31 % a les xarxes socials i el 8 % en la televisió.
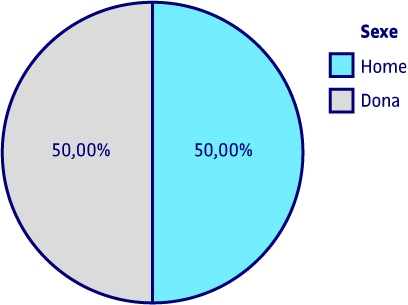
Les dades relatives a freqüències absolutes i/o percentatges es poden demanar en format de taula o gràfic. Quan la variable objecte d’estudi és qualitativa nominal i té poques categories, el gràfic més apropiat és el de sectors o circular. Si observem el gràfic, els resultats que mostra són els mateixos que ens dona la taula. Als següents gràfics de sectors o circulars s’aprecien els mateixos resultats que s’han mostrat en les taules corresponents.
Per a la variable dels diferents mitjans publicitaris, fem un diagrama de rectangles perquè, malgrat ser una variable qualitativa nominal, el fet de tenir més categories fa que aquest gràfic sigui més adequat que l’altre.
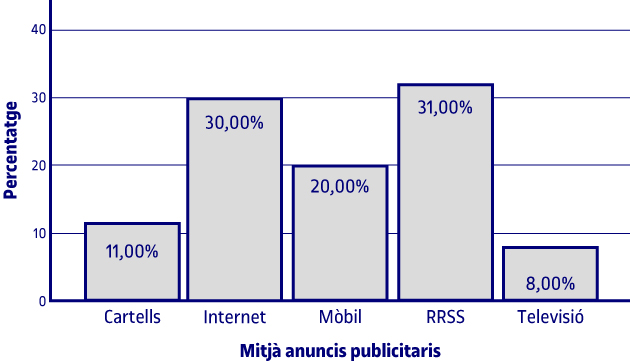
La informació que ens mostra el gràfic és la mateixa que la de la taula corresponent ja comentada.
Una vegada analitzades de manera descriptiva les variables qualitatives nominals, procedim a analitzar descriptivament les variables qualitatives ordinals del fitxer.
| Estadístics | ||||||
| Estudis que cursa | Estudis del pare | Estudis de la mare | Qualificació mitjana en estudis | Importància donada als diners | ||
| N | Vàlid | 100 | 100 | 98 | 100 | 97 |
| Perduts | 0 | 0 | 2 | 0 | 3 | |
| Mediana | 2,00 | 2,00 | 2,00 | 7,00 | 3,00 | |
| Moda | 2 | 2 | 2 | 7 | 2 | |
| Rang | 2 | 3 | 3 | 6 | 4 | |
| Mínim | 1 | 1 | 1 | 3 | 1 | |
| Màxim | 3 | 4 | 4 | 9 | 5 | |
| Percentils | 25 | 2,00 | 2,00 | 2,00 | 6,00 | 2,00 |
| 50 | 2,00 | 2,00 | 2,00 | 7,00 | 3,00 | |
| 75 | 3,00 | 3,00 | 3,00 | 7,00 | 4,00 | |
A la taula s’observa que per als estudis de la mare hi ha dos valors perduts i per a la importància que els alumnes donen als diners n’hi ha tres de perduts.
La mediana és el valor central de la variable després d’ordenar les dades de menor a major. S’observa que, per als estudis que cursa, el valor és 2, la qual cosa representa els estudis de 2n. cicle d’ESO – batxiller. La moda és 2, és a dir, el valor de la mediana coincideix amb el de la moda. El rang és 2. El rang és la diferència entre el valor màxim que pren la variable i el mínim. El percentil 25 és 2 i el 50 també (el percentil 50 sempre coincideix amb el valor de la mediana). En canvi, el percentil 75 és 3, i això vol dir que després d’ordenar les dades de menor a major el 75 % prenen com a molt el valor 3, que es correspon amb formació professional de grau mitjà.
Quant a la variable Estudis del pare i de la mare, ambdós tenen els mateixos estadístics de mediana 2, que coincideix amb la moda, és a dir, estudis primaris. El rang és de 3, perquè aquestes variables prenen valors d’1 a 4. El percentil 25 és 2 i el 50 també. En canvi, el percentil 75 és 3, i això vol dir que després d’ordenar les dades de menor a major el 75 % prenen com a molt el valor 3, que correspon a batxillerat o equivalents.
Si mirem la variable de qualificació mitjana en els estudis dels alumnes, la mediana pren el valor 7 igual que la moda. El rang és de 6 perquè la qualificació mitjana més baixa en els estudis és de 3 i la més alta de 9. El percentil 25 val 6, el 50 7 i el 75 7.
Finalment, la mediana de la importància que es dona als diners és 3, variable expressada en una escala de Likert de 5 punts, en sortir el valor de 3. Això vol dir que després d’ordenar les dades de menor a major valor el 50 % d’ells donen com a molt una importància mitjana als diners. La moda és 2, és a dir, el valor que es repeteix més en les respostes és que donen poca importància als diners. El rang és 4, perquè hem dit que és una variable de Likert de 5 punts i, per tant, pren valors de l’1 a 5. El percentil 25 val 2, el 50 3 i 75 4.
| Estudis que cursa | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Primària-1r.cicle ESO | 20 | 20,0 | 20,0 | 20,0 |
| 2n. cicle ESO-Batxillerat | 49 | 49,0 | 49,0 | 69,0 | |
| Form. prof. grau mitjà | 31 | 31,0 | 31,0 | 100,0 | |
| Total | 100 | 100,0 | 100,0 | ||
A la taula veiem que el 20 % dels alumnes cursen estudis de primària o de 1r. cicle d’ESO, el 49 % estudis de 2n. cicle d’ESO o batxillerat i el 31 % són alumnes de formació professional de grau mitjà.
| Estudis del pare | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Sense estudis | 14 | 14,0 | 14,0 | 14,0 |
| Estudis primaris | 37 | 37,0 | 37,0 | 51,0 | |
| Batxillerat o equivalents | 30 | 30,0 | 30,0 | 81,0 | |
| Diplomat, llicenciat o equivalents | 19 | 19,0 | 19,0 | 100,0 | |
| Total | 100 | 100,0 | 100,0 | ||
El 14 % dels pares dels alumnes enquestats no tenen estudis, el 37 % tenen estudis primaris, el 30 % tenen estudis de batxillerat o equivalents i el 19 % són diplomats, llicenciats o equivalents. A la taula anterior veiem que els percentatges coincideixen amb els percentatges vàlids perquè no hi havia valors perduts. Això no es repeteix a la taula que següent perquè hi ha valors perduts.
| Estudis de la mare | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Sense estudis | 6 | 6,0 | 6,1 | 6,1 |
| Estudis primaris | 59 | 59,0 | 60,2 | 66,3 | |
| Batxillerat o equivalents | 18 | 18,0 | 18,4 | 84,7 | |
| Diplomat, llicenciat o equivalents | 15 | 15,0 | 15,3 | 100,0 | |
| Total | 98 | 98,0 | 100,0 | ||
| Perduts | 9 | 2 | 2,0 | ||
| Total | 100 | 100,0 | |||
El 6 % de les mares dels alumnes enquestats no tenen estudis, el 59 % tenen estudis primaris, el 18 % tenen estudis de batxillerat o equivalents, el 15 % són diplomats, llicenciats o equivalents i del 2 % restant no es tenen dades, atès que els alumnes no les han aportat en l’enquesta que se’ls ha passat.
| Qualificació mitjana en estudis | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | 3 | 2 | 2,0 | 2,0 | 2,0 |
| 4 | 3 | 3,0 | 3,0 | 5,0 | |
| 5 | 16 | 16,0 | 16,0 | 21,0 | |
| 6 | 27 | 27,0 | 27,0 | 48,0 | |
| 7 | 33 | 33,0 | 33,0 | 81,0 | |
| 8 | 16 | 16,0 | 16,0 | 97,0 | |
| 9 | 3 | 3,0 | 3,0 | 100,0 | |
| Total | 100 | 100,0 | 100,0 | ||
Observant els percentatges acumulats, veiem que el 5 % dels alumnes tenen de mitjana una qualificació de no aprovat. Si mirem la columna dels percentatges, el 16 % tenen una qualificació mitjana de 5, el 27 % de 6, el 33 % de 7, el 16 % de 8 i el 3 % de 9.
| Importància que es dona als diners | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Molt poca | 8 | 8,0 | 8,2 | 8,2 |
| Poca | 32 | 32,0 | 33,0 | 41,2 | |
| Mitjana | 19 | 19,0 | 19,6 | 60,8 | |
| Molta | 19 | 19,0 | 19,6 | 80,4 | |
| Moltíssima | 19 | 19,0 | 19,6 | 100,0 | |
| Total | 97 | 97,0 | 100,0 | ||
| Perduts | 9 | 3 | 3,0 | ||
| Total | 100 | 100,0 | |||
Pel que fa a la importància que els alumnes donen als diners, s’observa que el 8 % n’hi donen molt poca, el 32 % poca, el 19 % mitjana, el 19 % molta, el 19 % moltíssima, i el 3 % no contesta a la pregunta.
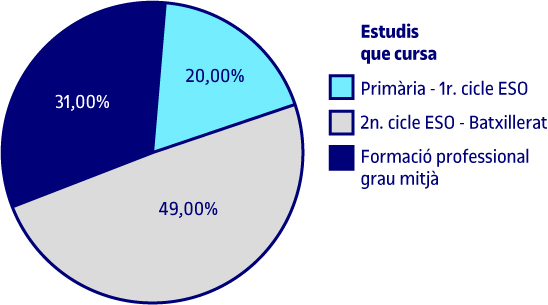
Com ja s’ha comentat anteriorment, les dades relatives a freqüències absolutes o percentatges es poden demanar en format de taula o gràfic. Quan la variable objecte d’estudi és qualitativa ordinal i de poques categories, el gràfic més apropiat és el de sectors o circular. Si observem el gràfic, els resultats que mostra són els mateixos que ens dona la taula. Als següents gràfics de sectors o circulars s’aprecien els mateixos resultats que s’han mostrat a les taules corresponents.
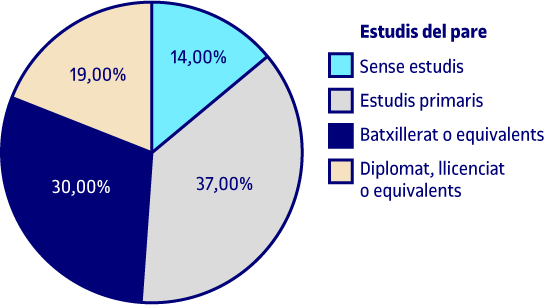
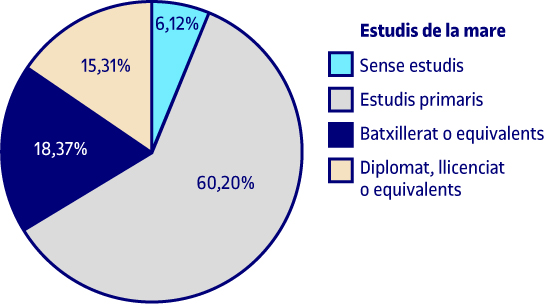
Per a la variable de la qualificació mitjana dels estudis i de la importància que donen als diners, fem un diagrama de rectangles perquè, malgrat ser una variable qualitativa ordinal, el fet de tenir més categories fa que aquest gràfic sigui més adequat que l’altre.
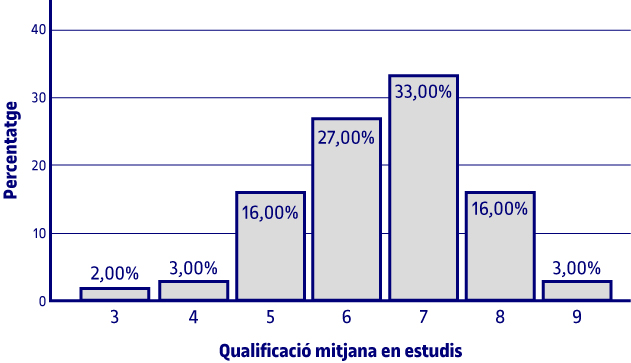
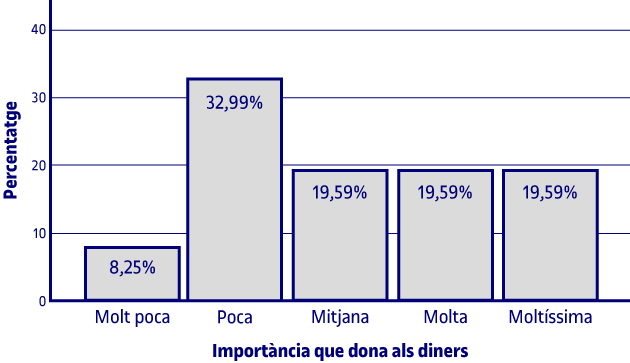
La informació que els gràfics ens mostren és la mateixa que la de la taula corresponent ja comentada.
Una vegada analitzades de manera descriptiva les variables qualitatives ordinals, procedim a analitzar descriptivament les variables quantitatives del fitxer. La paga setmanal en euros s’ha considerat variable quantitativa contínua, encara que si s’observen les dades d’aquesta variable en realitat és una variable quantitativa discreta. Això ens permet poder triar entre fer un diagrama de barres o un histograma a l’hora de fer el gràfic associat a aquesta variable. El nombre de germans, inclòs el subjecte, és una variable quantitativa discreta. L’edat és una variable quantitativa discreta, tal com apareix en les dades, encara que es podria considerar també com a variable quantitativa contínua. Però no és molt habitual que, quan a algú li preguntin per la seva edat, respongui, per exemple, 14,5 anys.
| Estadístics | ||||
| Paga setmanal en euros | Nre. de germans inclòs subjecte | Edat | ||
| N | Vàlid | 92 | 100 | 100 |
| Perduts | 8 | 0 | 0 | |
| Mitjana | 12,95 | 2,74 | 15,79 | |
| Error estàndard de la mitjana | ,453 | ,135 | ,168 | |
| Mediana | 11,00 | 2,50 | 16,00 | |
| Moda | 10 | 2 | 16 | |
| Desviació | 4,348 | 1,346 | 1,684 | |
| Variància | 18,909 | 1,811 | 2,834 | |
| Asimetria | ,814 | ,946 | -,193 | |
| Error estàndard d’asimetria | ,251 | ,241 | ,241 | |
| Curtosi | -,620 | ,945 | ,054 | |
| Error estàndard de curtosi | ,498 | ,478 | ,478 | |
| Rang | 14 | 6 | 8 | |
| Mínim | 8 | 1 | 12 | |
| Màxim | 22 | 7 | 20 | |
| Suma | 1191 | 274 | 1579 | |
| Percentils | 25 | 10,00 | 2,00 | 15,00 |
| 50 | 11,00 | 2,50 | 16,00 | |
| 75 | 16,00 | 3,00 | 17,00 | |
Si estudiem la variable Paga setmanal en euros, veiem a la taula que hi ha 8 dades perdudes; per tant, només 92 vàlides. La mitjana val 12,95 euros, amb un error estàndard de la mitjana de 0,453 euros. La mediana és d’11 euros, la moda és de 10 euros, és a dir, donen 10 euros a la majoria, la quasidesviació típica és 4,348 i la quasivariància és de 18,909.
Nota. La desviació estàndard (SD) representa la variació en els valors d’una variable, mentre que l’error estàndard de la mitjana (standard error of the mean, SEM) representa la dispersió que tindria la mitjana d’una mostra de valors si es continuessin prenent mostres. Per tant, el SEM proporciona una idea de la precisió de la mitjana i l’SD ens dona una idea de la variabilitat de les observacions individuals. Aquests dos paràmetres estan relacionats:

L’important és indicar el valor de la desviació típica, no de l’error estàndard de la mitjana.


El coeficient d’asimetria val 0,814, i això vol dir que la distribució de la mostra presenta una asimetria positiva o per la dreta.
Nota asimetria. Aquesta mesura ens permet identificar si les dades es distribueixen de manera uniforme al voltant del punt central (mitjana aritmètica). L’asimetria presenta tres estats diferents, cadascun dels quals defineix de manera concisa com estan distribuïdes les dades respecte a l’eix d’asimetria. Es diu que l’asimetria és positiva quan la majoria de les dades estan per sobre del valor de la mitjana aritmètica, la corba és simètrica quan es distribueixen aproximadament la mateixa quantitat de valors en tots dos costats de la mitjana, i hi ha asimetria negativa quan la major quantitat de dades s’aglomeren en els valors menors que la mitjana.
![]() coeficient d’asimetria de Fisher.
coeficient d’asimetria de Fisher.
Si ![]() , la distribució és simètrica, és a dir, hi ha aproximadament la mateixa quantitat de valors als dos costats de la mitjana. Aquest valor és difícil d’aconseguir i per això es tendeix a prendre els valors que són propers, positius o negatius (± 0,5).
, la distribució és simètrica, és a dir, hi ha aproximadament la mateixa quantitat de valors als dos costats de la mitjana. Aquest valor és difícil d’aconseguir i per això es tendeix a prendre els valors que són propers, positius o negatius (± 0,5).
Si ![]() , la corba és asimètricament positiva i per això els valors es tendeixen a reunir més à la part esquerra de la mitjana que a la dreta.
, la corba és asimètricament positiva i per això els valors es tendeixen a reunir més à la part esquerra de la mitjana que a la dreta.
Si ![]() , la corba és asimètricament negativa i per això els valors es tendeixen a reunir més a la part dreta de la mitjana.
, la corba és asimètricament negativa i per això els valors es tendeixen a reunir més a la part dreta de la mitjana.
Com més gran sigui el nombre (positiu o negatiu), major serà la distància que separa l’aglomeració dels valors pel que fa a la mitjana.
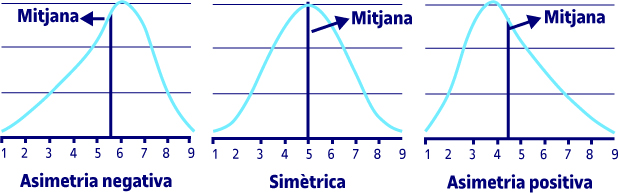
El fet que la curtosi sigui de −0,620 vol dir que la mostra és platicúrtica.
Nota de la curtosi. Aquesta mesura determina el grau de concentració que presenten els valors a la regió central de la distribució. Per mitjà del coeficient de curtosi, podem identificar si hi ha una gran concentració de valors (leptocúrtica), una concentració normal (mesocúrtica) o una concentració baixa (platicúrtica).
![]() coeficient d’excés (o de Fisher)
coeficient d’excés (o de Fisher)
Si ![]() , la distribució és mesocúrtica. Igual que en l’asimetria, és bastant difícil trobar un coeficient de curtosi de valor zero, per la qual cosa se solen acceptar els valors propers (± 0,5 aprox.).
, la distribució és mesocúrtica. Igual que en l’asimetria, és bastant difícil trobar un coeficient de curtosi de valor zero, per la qual cosa se solen acceptar els valors propers (± 0,5 aprox.).
Si ![]() , la distribució és leptocúrtica.
, la distribució és leptocúrtica.
Si ![]() , la distribució és platicúrtica.
, la distribució és platicúrtica.
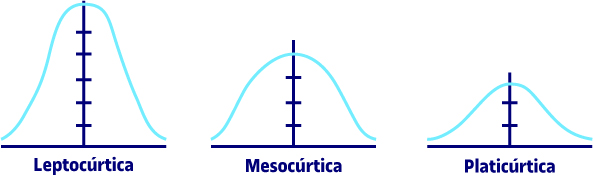
Quan la distribució de les dades té un coeficient d’asimetria (![]() = ±0,5) i un coeficient de curtosi de
= ±0,5) i un coeficient de curtosi de ![]() = ±0,5), es denomina «corba normal». Aquest criteri és molt important, ja que per a la majoria dels procediments de l’estadística d’inferència es requereix que les dades es distribueixin normalment.
= ±0,5), es denomina «corba normal». Aquest criteri és molt important, ja que per a la majoria dels procediments de l’estadística d’inferència es requereix que les dades es distribueixin normalment.
El principal avantatge de la distribució normal rau en el supòsit que el 95 % dels valors està en una distància de dues desviacions estàndards de la mitjana aritmètica; és a dir, si prenem la mitjana i li sumem dues vegades la desviació i després en restem dues desviacions, el 95 % dels casos estaria dins del rang que componen aquests valors.
El valor mínim és 8 euros i el màxim és 22 euros. La diferència es coneix com a rang. S’observa que entre el percentil 25 i 50 hi ha poca diferència quant a valor, i això vol dir que la meitat de la mostra rep 11 euros de paga com a molt.
Si estudiem la variable Nombre de germans, inclòs el subjecte, podem mirar la taula i veure que no hi ha dades perdudes; per tant, n’hi ha 100 de vàlids. La mitjana i la mediana valen aproximadament tres germans, amb un error estàndard de la mitjana aproximadament de 0, la moda 2; és a dir, la majoria té dos germans. La quasidesviació típica val aproximadament 1, la quasivariància pren aproximadament el valor 2.
La desviació típica es calcularia així: ![]()
El coeficient d’asimetria val 0,946, i vol dir que la distribució de la mostra presenta una asimetria positiva o per la dreta. El fet que la curtosi sigui de 0,945 vol dir que la mostra és lectocúrtica. El valor mínim és d’un germà i el màxim és de set. La diferència és el que es coneix com a rang. S’observa que entre els tres percentils hi ha poca diferència quant a valor, i això vol dir que el 75 % dels alumnes de la mostra té tres germans com a molt.
Si estudiem la variable Edat, mirant la taula veiem que no hi ha dades perdudes; per tant, n’hi ha 100 de vàlids. La mitjana val 15,79 anys, amb un error estàndard de la mitjana de 0,168 anys. La mediana i la moda són 16 anys; és a dir, la majoria tenen 16 anys. La quasidesviació típica és 1,684, la quasivariància és de 2,834.
![]()
El coeficient d’asimetria val −0,193 i la curtosi val 0,054, i això vol dir que la mostra de la variable Edat es pot considerar que s’ajusta a una corba normal. El valor mínim és 12 i el màxim és 20 anys. La diferència és el que es coneix com a rang. S’observa que entre els tres percentils hi ha poca diferència quant a valor, i això vol dir que el 75 % dels alumnes de la mostra té disset anys com a molt.
A continuació es mostren els resultats referits als percentatges dels diferents valors que prenen les variables quantitatives discretes gràficament. Donada la classificació d’aquestes variables, el tipus de gràfic a demanar és un diagrama de barres.
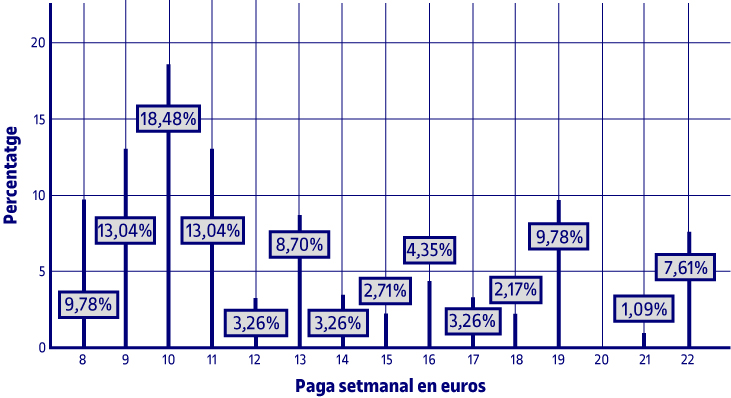
En la gràfica s’observa, per exemple, que el valor més repetit de diners rebuts com a paga setmanal és de 10 euros, valor que coincideix amb el de la moda i amb el fet que ningú no rep 20 euros com a paga setmanal.
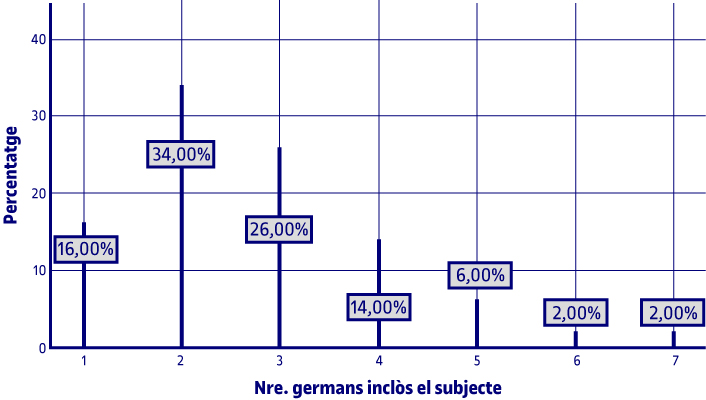
A la gràfica s’observa, per exemple, que el valor de nombre de germans més repetit, incloent-hi el subjecte, és 2, que coincideixi amb el valor de la moda. Una altra dada que s’observa és, per exemple, que el 2 % té sis germans, inclòs ell, i aquest percentatge es repeteix per als que tenen set germans, inclosos ells.
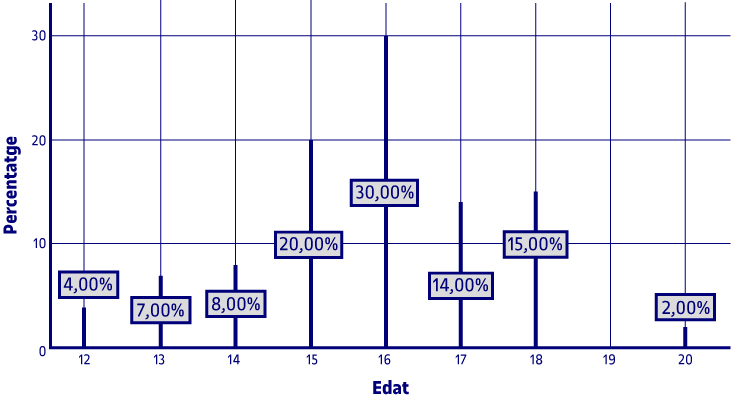
A la gràfica s’observa, per exemple, que el valor d’edat més repetit és 16, que coincideixi amb el valor de la moda. Una altra dada que s’observa és, per exemple, que ningú no té dinou anys.
Si haguéssim considerat la paga setmanal en euros com a quantitativa contínua, s’hauria d’haver dut a terme un histograma en lloc d’un gràfic de barres.
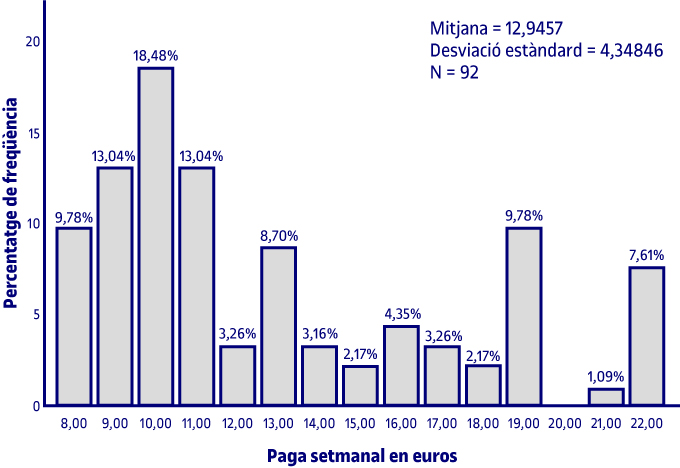
En l’histograma et calcula, a més dels percentatges dels diferents valors que pren la variable, la mitjana i la quasidesviació típica.
Per a les variables quantitatives contínues, podem demanar, a més de l’histograma, que ens dibuixi el seu ajustament a diferents distribucions, una de les quals és la normal.
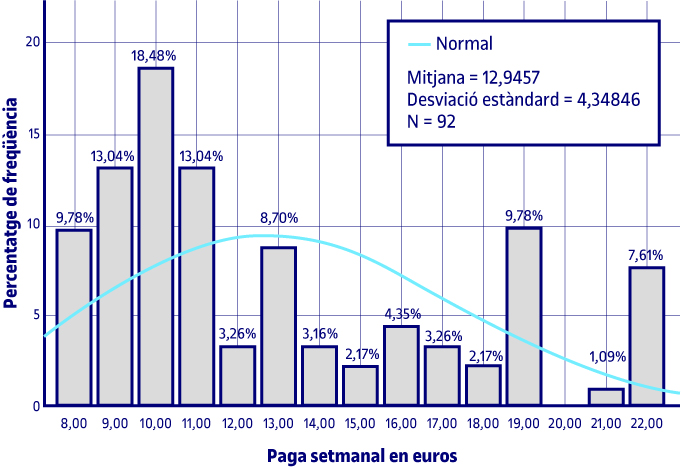
A la gràfica s’observa que la distribució de les dades de la paga setmanal en euros és platicúrtica i que té asimetria positiva o per la dreta.
Si haguéssim fet un histograma per a la variable Edat amb l’estudi de l’ajustament de la distribució d’aquesta variable a una corba normal, el gràfic requerit seria el següent:
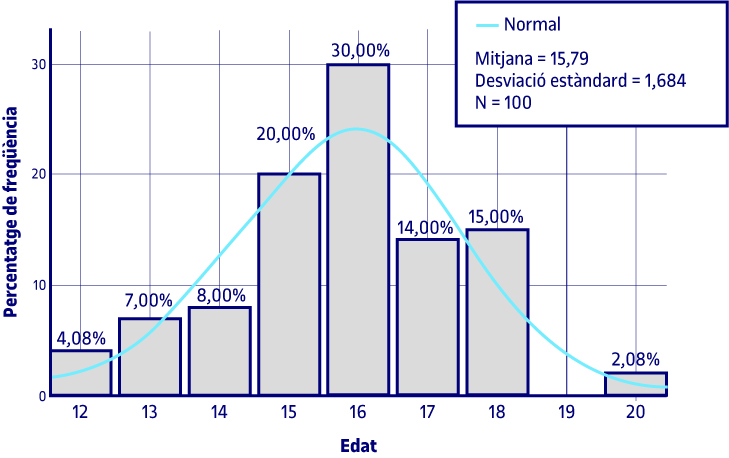
S’hi aprecia que la distribució de la variable Edat s’ajusta a una corba normal.
Encara que hi ha més variables relacionades entre elles, ens limitarem a estudiar les variables que estan relacionades de manera directa o inversa amb els mitjans en què es veuen els anuncis publicitaris per intentar establir un perfil per a cada tipus de mitjà. Si mirem la taula, veiem que per a un nivell de confiança del 99 % està relacionada amb l’edat; a més, en tenir un valor de 0,475, la relació és directa, és a dir, que com més edat més gran és el nombre amb què es veu publicitat en un mitjà codificat. Així, per a les edats més baixes el mitjà seran els cartells, i per a les edats més elevades, la televisió.
Com que veiem que està relacionada amb l’edat, demanarem la recta de regressió lineal considerant com a variable dependent la variable dels mitjans on es veuen anuncis publicitaris, i com a independent l’edat.
| Variables entrades/eliminadesa | |||
| Model | Variables entrades | Variables eliminades | Mètode |
| 1 | Edatb | . | Introduir |
Aquesta taula ens indica la variable que ha entrat en el model, que és la identificada com a correlacionada amb la dependent.
| Resum del model | ||||
| Model | R | R quadrat | R quadrat ajustat | Error estàndard de l’estimació |
| 1 | ,475a | ,225 | ,217 | 1,040 |
Si observem el resum del model, el coeficient de determinació (R quadrat) és el de correlació al quadrat i val 0,225, la qual cosa significa que el 22,5 % de la variabilitat de la variable Mitjans està representada per la recta de regressió.
| ANOVAa | ||||||
| Model | Suma de quadrats | gl | Mitjana quadràtica | F | Sig. | |
| 1 | Regressió | 30,791 | 1 | 30,791 | 28,478 | ,000b |
| Residu | 105,959 | 98 | 1,081 | |||
| Total | 136,750 | 99 | ||||
Un dels errors típics és no tenir clar què significa acceptar o rebutjar la hipòtesi nul·la (![]() ).
).
Quan el resultat d’un contrast d’hipòtesi és rebuig d’hipòtesi nul·la, la hipòtesi és falsa; per contra, acceptar la hipòtesi nul·la significa que no es té la suficient informació per poder rebutjar-la (és a dir, que potser amb una altra mostra o augmentant-ne la grandària el resultat seria diferent, cosa que no passa quan es rebutja la hipòtesi nul·la).
Direm que un valor és molt significatiu si té poca probabilitat d’ocórrer o aparèixer, i un contrast és significatiu quan es rebutja ![]() .
.
![]() No hi ha regressió.
No hi ha regressió.
![]()
![]() (hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
(hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
El contrast que fem és que no hi ha regressió. Com que el p-valor val 0, el contrast és significatiu i, per tant, sí que té sentit fer la recta de regressió.
| Coeficientsa | ||||||
| Model | Coeficients no estandarditzats | Coeficients estandarditzats | t | Sig. | ||
| B | Desv. Error | Beta | ||||
| 1 | (Constant) | -2,281 | ,986 | -2,314 | ,023 | |
| Edat | ,331 | ,062 | ,475 | 5,337 | ,000 | |
![]() Els coeficients són nuls.
Els coeficients són nuls.
![]()
![]() (hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
(hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
Ens queda escriure l’equació de la recta de regressió. Veient la taula, la recta de regressió és: ![]() . Com que el p-valor associat a la constant és 0,023 ≤ 0,05 i l’associat al coeficient de l’edat també és menor que 0,05 per a un nivell de confiança del 95 %, la constant i el coeficient de la variable Edat són no nuls.
. Com que el p-valor associat a la constant és 0,023 ≤ 0,05 i l’associat al coeficient de l’edat també és menor que 0,05 per a un nivell de confiança del 95 %, la constant i el coeficient de la variable Edat són no nuls.
Per aprofundir
A continuació s’ha treballat amb les dades del fitxer RRSS i fent ús de l’SPSS (es poden fer els càlculs amb la versió gratuïta del PSPP), es mostren les sortides del programa i les interpretacions de tots els resultats estadístics als quals s’ha fet referència de manera teòrica anteriorment.
En aquest cas la grandària de la mostra ha estat de 75 alumnes.
A la primera taula s’observen els valors dels estadístics de les variables qualitatives nominals del fitxer.
| Estadístics | |||||
| Sexe | Tipus de centre d’estudis | Hàbitat | Xarxes socials codificades | ||
| N | Vàlid | 75 | 75 | 75 | 75 |
| Perduts | 0 | 0 | 0 | 0 | |
| Moda | 2 | 1 | 2 | 7 | |
Veiem que per a totes les variables la grandària de la mostra és de 75 i no hi ha valors perduts. La moda de la variable Sexe és 2; és a dir, en la mostra hi ha més dones que homes. Per al tipus de centre d’estudis, el valor de la variable que es repeteix més és el 1; és a dir, hi ha més centres públics que privats. L’hàbitat més repetit és el que pren el valor 2, és a dir, urbà, i la xarxa social més utilitzada en les respostes dels enquestats és el que pren el valor 7 en la codificació; és a dir, que la xarxa social més de moda entre els enquestats és YouTube.
| Sexe | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Home | 27 | 36,0 | 36,0 | 36,0 |
| Dona | 48 | 64,0 | 64,0 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
Quant al sexe dels enquestats, el 36 % són homes i el 64 % són dones.
| Tipus de centre d’estudis | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Públic | 56 | 74,7 | 74,4 | 74,7 |
| Privat | 19 | 25,3 | 25,3 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
Anteriorment s’ha comentat que havien estat seleccionats més centres públics que privats; en concret, hi ha 56 centres públics i 19 centres privats. Com que la mostra és de grandària 75, la freqüència absoluta no coincideix amb el percentatge. En no haver-hi dades perdudes, el percentatge per a cada tipus de centre d’estudis coincideix amb el percentatge vàlid.
| Hàbitat | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Rural | 20 | 26,7 | 26,7 | 26,7 |
| Urbà | 55 | 73,3 | 73,3 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
Pel que fa a l’hàbitat, la taula anterior ens indicava que hi havia més centres urbans que rurals; en concret, hi ha 55 centres urbans i 20 de rurals.
| Xarxa social més usada | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | 11 | 14,7 | 14,7 | 14,7 | |
| 14 | 18,7 | 18,7 | 33,3 | ||
| Snapchat | 5 | 6,7 | 6,7 | 40,0 | |
| TikTok | 13 | 17,3 | 17,3 | 57,3 | |
| 3 | 4,0 | 4,0 | 61,3 | ||
| 13 | 17,3 | 17,3 | 78,7 | ||
| YouTube | 16 | 21,3 | 21,3 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
Les xarxes socials que usen majoritàriament els alumnes són Facebook, Instagram, Snapchat, TikTok, Twitter, WhatsApp i YouTube. El 14,7 % d’ells usen majoritàriament Facebook, el 18,7 % Instagram, el 6,7 % Snapchat, el 17,3 % TikTok, el 4 % Twitter, el 17,3 % WhatsApp i el 21,3 % Facebook.
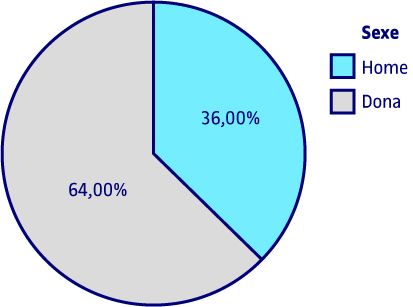
Les dades relatives a freqüències absolutes o percentatges es poden demanar en format de taula o gràfic. Quan la variable objecte d’estudi és qualitativa nominal i té poques categories, el gràfic més apropiat és el de sectors o circular. Si observem el gràfic, els resultats que mostra són els mateixos que ens dona la taula. En els següents gràfics de sectors o circulars s’aprecien els mateixos resultats que es van mostrar a les taules corresponents.
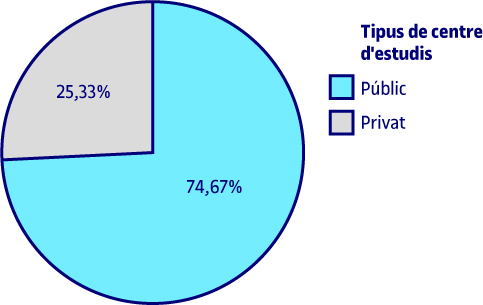
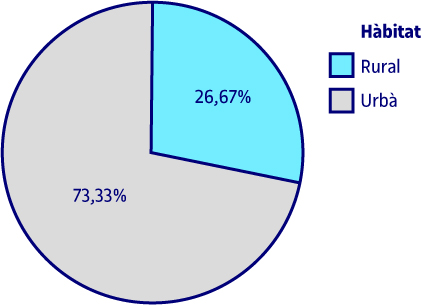
Per a la variable de les diferents xarxes socials fem un diagrama de rectangles, perquè, malgrat ser una variable qualitativa nominal, el fet de tenir més categories fa que aquest gràfic sigui més adequat que l’altre.
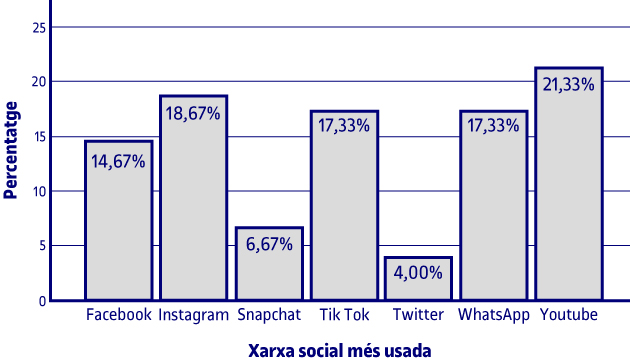
La informació que ens mostra el gràfic és la mateixa que la de la taula corresponent comentada anteriorment.
Una vegada analitzades de manera descriptiva les variables qualitatives nominals, procedim a analitzar descriptivament les variables qualitatives ordinals del fitxer.
| Estadístics | ||||||
| Estudis que cursa | Estudis del pare | Estudis de la mare | Qualificació mitjana en estudis | Importància donada als diners | ||
| N | Vàlid | 75 | 75 | 75 | 75 | 75 |
| Perduts | 0 | 0 | 0 | 0 | 0 | |
| Mediana | 2,00 | 3,00 | 3,00 | 6,00 | 4,00 | |
| Moda | 2 | 3 | 3 | 7 | 4 | |
| Rang | 2 | 3 | 3 | 6 | 4 | |
| Mínim | 1 | 1 | 1 | 3 | 1 | |
| Màxim | 3 | 4 | 4 | 9 | 5 | |
| Percentils | 25 | 1,00 | 2,00 | 2,00 | 5,00 | 2,00 |
| 50 | 2,00 | 3,00 | 3,00 | 6,00 | 4,00 | |
| 75 | 3,00 | 3,00 | 3,00 | 7,00 | 4,00 | |
A la taula s’observa que no hi ha valors perduts per cap de les variables considerades.
La mediana és el valor central de la variable. Després d’ordenar les dades de menor a major, s’observa que el valor és de 2per als estudis que cursa, la qual cosa representa els estudis de 2n. cicle d’ESO – batxiller. La moda és 2; és a dir, el valor de la mediana coincideix amb el de la moda. El rang és 2 (el rang és la diferència entre el valor màxim que pren la variable i el mínim). El percentil 25 és 1 i el 50 és 2 (el percentil 50 coincideix amb el valor de la mediana sempre). El percentil 75 és 3, i això vol dir que després d’ordenar les dades de menor a major, el 75 % prenen el valor 3 com a molt, que es correspon amb formació professional de grau mitjà.
Quant a les variables Estudis del pare i de la mare, ambdues tenen els mateixos estadístics, de mediana 3, que coincideix amb la moda, és a dir, batxiller o equivalents. El rang és de 3 perquè aquestes variables prenen valors d’1 a 4. El percentil 25 és 2 i el 50 és 3, que coincideix amb el fet que percentil 75 és 3; això vol dir que després d’ordenar les dades de menor a major el 75 % prenen el valor 3 com a molt, que es correspon a batxillerat o equivalents.
Si mirem la variable Qualificació mitjana en els estudis dels alumnes, la mediana pren el valor 6 i la moda de 7. El rang és de 6 perquè la qualificació mitjana en els estudis més baixa és de 3 i la més alta de 9. El percentil 25 val 5, el 50 6, i 75 7.
Finalment, la mediana de la importància que es dona als diners és 4, i aquesta és una variable expressada en una escala de Likert de 5 punts. En sortir el valor de 4, després d’ordenar les dades de menor a major valor el 50 % donen com a molt importància als diners. La moda és 4; és a dir, el valor que repeteix es més en les respostes és que donen molta importància als diners. El rang és 4 perquè hem comentat que és una variable de Likert de 5 punts; per tant, pren valors d’1 a 5. El percentil 25 val 2 i el 50 4, igual que el percentil 75.
| Estudis que cursa | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Primària-1r. cicle ESO | 19 | 25,3 | 25,3 | 25,3 |
| 2n. cicle ESO-Batxillerat | 34 | 45,3 | 45,3 | 70,7 | |
| Formació prof. grau mitjà | 22 | 29,3 | 29,3 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
A la taula veiem que el 25,3 % dels alumnes cursen estudis de primària o de 1r. cicle d’ESO, el 45,3 % estudis de 2n. cicle d’ESO o batxillerat i el 29,3 % són alumnes de formació professional de grau mitjà.
| Estudis del pare | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Sense estudis | 5 | 6,7 | 6,7 | 6,7 |
| Estudis primaris | 29 | 38,7 | 38,7 | 45,3 | |
| Batxillerat o equivalents | 30 | 40,0 | 40,0 | 85,3 | |
| Diplomat, llicenciat o equivalents | 11 | 14,7 | 14,7 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
El 6,7 % dels pares dels alumnes enquestats no tenen estudis, el 38,7 % tenen estudis primaris, el 40 % estudis de batxillerat o equivalents i el 14,7 % són diplomats, llicenciats o equivalents.
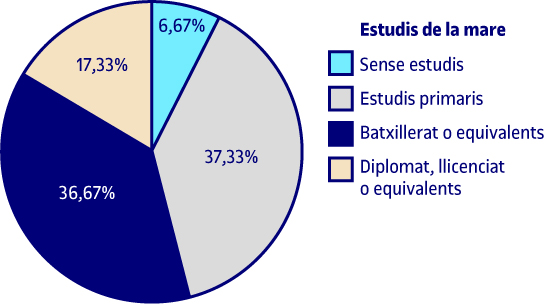
| Estudis de la mare | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Sense estudis | 5 | 6,7 | 6,7 | 6,7 |
| Estudis primaris | 28 | 37,3 | 37,3 | 44,0 | |
| Batxillerat o equivalents | 29 | 38,7 | 38,7 | 82,7 | |
| Diplomat, llicenciat o equivalents | 13 | 17,3 | 17,3 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
El 6,7 % de les mares dels alumnes enquestats no tenen estudis, el 37,3 % tenen estudis primaris, el 38,7 % estudis de batxillerat o equivalents, i el 17,3 % són diplomats, llicenciats o equivalents.
| Qualificació mitjana en estudis | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | 3 | 2 | 2,7 | 2,7 | 2,7 |
| 4 | 1 | 1,3 | 1,3 | 4,0 | |
| 5 | 17 | 22,7 | 22,7 | 26,7 | |
| 6 | 21 | 28,0 | 28,0 | 54,7 | |
| 7 | 24 | 32,0 | 32,0 | 86,7 | |
| 8 | 9 | 12,0 | 12,0 | 98,7 | |
| 9 | 1 | 1,3 | 1,3 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
Si observem els percentatges acumulats, veiem que el 4 % dels alumnes tenen una qualificació mitjana de no aprovat. Si mirem la columna dels percentatges, el 22,7 % tenen una qualificació mitjana de 5, el 28 % de 6, el 32 % de 7, el 12 % de 8 i el 1,3 % de 9.
| Importància que es dona als diners | |||||
| Freqüència | Percentatge | Percentatge vàlid | Percentatge acumulat | ||
| Vàlid | Molt poca | 1 | 1,3 | 1,3 | 1,3 |
| Poca | 18 | 24,0 | 24,0 | 25,3 | |
| Mitjana | 17 | 22,7 | 22,7 | 48,0 | |
| Molta | 21 | 28,0 | 28,0 | 76,0 | |
| Moltíssima | 18 | 24,0 | 24,0 | 100,0 | |
| Total | 75 | 100,0 | 100,0 | ||
Pel que fa a la importància que els alumnes donen als diners, s’observa que el 1,3 % n’hi donen molt poca, el 24 % poca, el 22,7 % mitjana, el 28 % molta i el 24 % moltíssima.
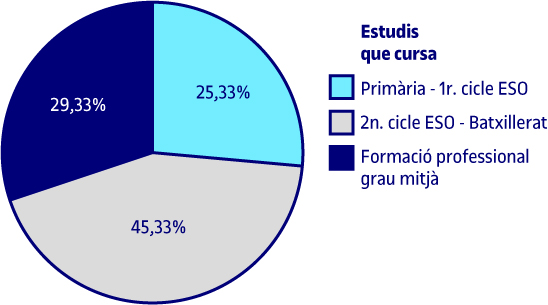
Com ja s’ha comentat anteriorment, les dades relatives a freqüències absolutes o percentatges es poden demanar en format de taula o gràfic. Quan la variable objecte d’estudi és qualitativa ordinal i de poques categories, el gràfic més apropiat és el de sectors o circular. Si observem el gràfic, els resultats que mostra són els mateixos que ens dona la taula. Als següents gràfics de sectors o circulars s’aprecien els mateixos resultats que es van mostrar a les taules corresponents.
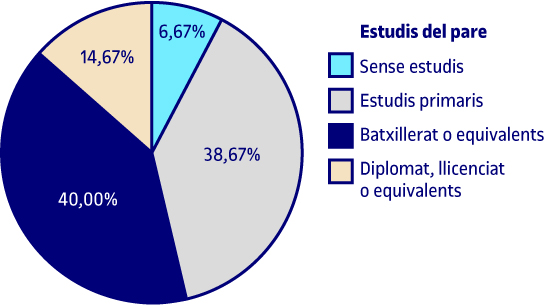
Per a la variable de la qualificació mitjana dels estudis i de la importància que es dona als diners, fem un diagrama de rectangles perquè, malgrat ser una variable qualitativa ordinal, el fet de tenir més categories fa que aquest gràfic sigui més adequat que l’altre.
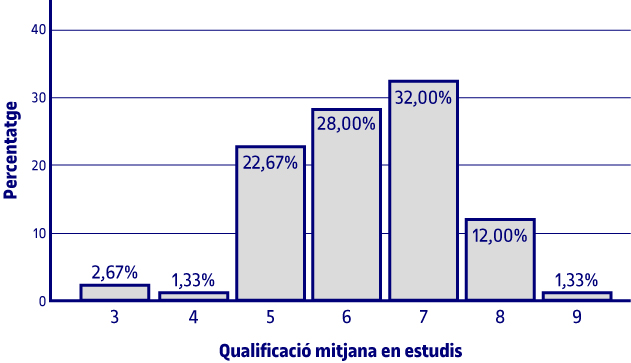
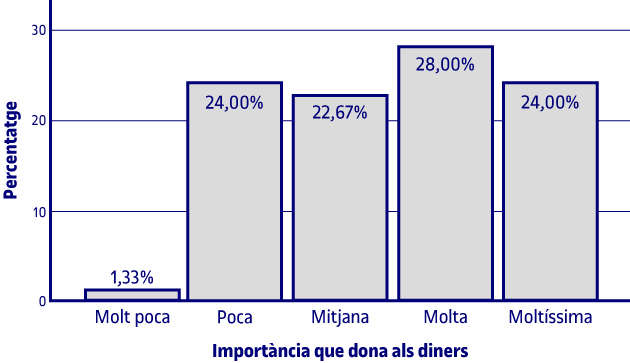
La informació que ens mostren els gràfics és la mateixa que la de la taula corresponent comentada anteriorment.
Una vegada analitzades de manera descriptiva les variables qualitatives ordinals, procedim a analitzar descriptivament les variables quantitatives del fitxer. La paga setmanal en euros s’ha considerat variable quantitativa contínua, encara que, si s’observen les dades d’aquesta variable, en realitat és variable quantitativa discreta; això ens permet triar entre fer un diagrama de barres o un histograma a l’hora de fer el gràfic associat a aquesta variable. El nombre de germans, inclòs el subjecte, és una variable quantitativa discreta. L’edat és una variable quantitativa discreta, tal com apareix en les dades, encara que es podria considerar també com a variable quantitativa contínua, però no és molt habitual, com ja es va comentar a l’exemple anterior sobre publicitat.
| Estadístics | ||||
| Paga setmanal en euros | Nre. de germans inclòs el subjecte | Edat | ||
| N | Vàlid | 75 | 75 | 75 |
| Perduts | 0 | 0 | 0 | |
| Mitjana | 16,2800 | 2,63 | 15,71 | |
| Error estàndard de la mitjana | ,51729 | ,177 | ,229 | |
| Mediana | 17,0000 | 2,00 | 16,00 | |
| Moda | 22,00 | 2 | 16 | |
| Desviació | 4,47986 | 1,531 | 1,985 | |
| Variància | 20,069 | 2,345 | 3,940 | |
| Asimetria | -,360 | 1,284 | -,134 | |
| Error estàndard d’asimetria | ,277 | ,277 | ,277 | |
| Curtosi | -1,120 | 1,398 | -,374 | |
| Error estàndard de curtosi | ,548 | ,548 | ,548 | |
| Rang | 14,00 | 6 | 8 | |
| Mínim | 8,00 | 1 | 12 | |
| Màxim | 22,00 | 7 | 20 | |
| Suma | 1221,00 | 197 | 1178 | |
| Percentils | 25 | 12,0000 | 2,00 | 15,00 |
| 50 | 17,0000 | 2,00 | 16,00 | |
| 75 | 19,0000 | 3,00 | 17,00 | |
Si estudiem la variable Paga setmanal en euros, a la taula veiem que no hi ha dades perdudes; per tant, són 75 vàlids. La mitjana val 16,28 euros, amb un error estàndard de la mitjana de 0,52 euros aproximadament. La mediana és de 17 euros. La moda és de 22 euros, és a dir, a la majoria li donen 22 euros. La quasidesviació típica és aproximadament 4,48, i la quasivariància és 20,069.
L’important és indicar el valor de la desviació típica, no de l’error estàndard de la mitjana.


El coeficient d’asimetria val −0,36, i això vol dir que la distribució de la mostra presenta una asimetria negativa o per l’esquerra.
El fet que la curtosi sigui de −0,120 vol dir que la mostra és platicúrtica.
El valor mínim és 8 euros i el màxim és 22 euros, i la diferència és el que es coneix com a rang. S’observa que entre els percentils 25 i 50 hi ha molta diferència quant a valor i que no n’hi ha tanta entre el 50 i el 75.
Si estudiem la variable Nombre de germans inclòs el subjecte, a la taula veiem que no hi ha dades perdudes; per tant, hi ha 75 vàlids. La mediana i la moda valen aproximadament 2; és a dir, la majoria té dos germans. La quasidesviació típica val aproximadament 2, i la quasivariància pren el valor 2 aproximadament.
La desviació típica es calcularia així: 
El coeficient d’asimetria val 1,284, i això vol dir que la distribució de la mostra presenta una asimetria positiva o per la dreta. El fet que la curtosi sigui de 1,398 vol dir que la mostra és lectocúrtica. El valor mínim és d’1 germà i el màxim és de 7, i diferència és el rang. S’observa que entre els tres percentils hi ha poca diferència quant a valor, i això vol dir que el 75 % dels alumnes de la mostra té tres germans com a molt.
Si estudiem la variable Edat, a la taula veiem que no hi ha dades perdudes; per tant, hi ha 75 vàlids. La mitjana val 15,71 anys, amb un error estàndard de la mitjana de 0,229 anys. La mediana i la moda són 16 anys; és a dir, la majoria tenen 16 anys. La quasidesviació típica és 1,985, i la quasivariància és 3,94.

El coeficient d’asimetria val −0,134 i la curtosi val −0,374, i això vol dir que es pot considerar que la mostra de la variable Edat s’ajusta a una corba normal. El valor mínim és 12 anys i el màxim és 20 anys, i la diferència és el rang. S’observa que entre els tres percentils hi ha poca diferència quant a valor, i això vol dir que el 75 % dels alumnes de la mostra té 17 anys com a molt.
A continuació es mostren els resultats referits als percentatges dels diferents valors que prenen les variables quantitatives gràficament. Donada la classificació d’aquestes variables, el tipus de gràfic que es demana és un diagrama de barres per a les discretes i l’histograma per a les quantitatives contínues.
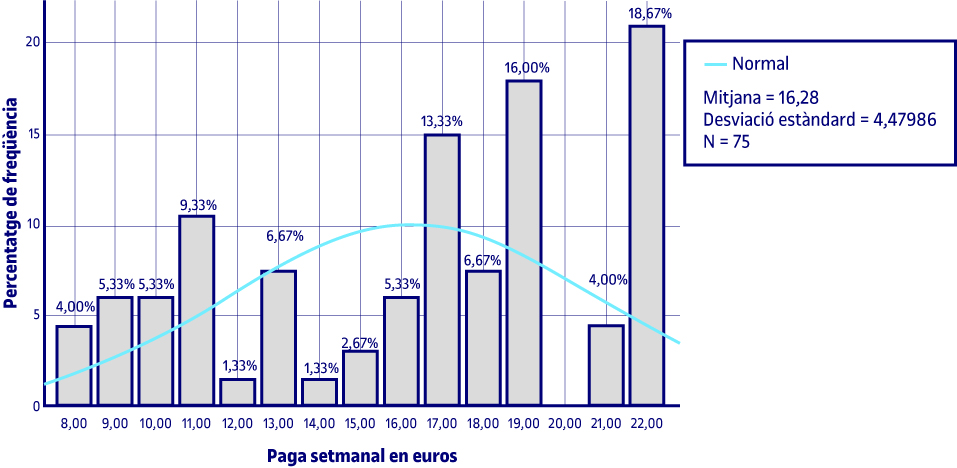
A l’histograma es calcula la mitjana i la quasidesviació típica, a més dels percentatges dels diferents valors que pren la variable. S’observa que la majoria reben 22 euros, i per aquest motiu això és el que val la moda, i que ningú no rep 20 euros de paga.
A la gràfica s’observa que la distribució de les dades de la paga setmanal en euros és platicúrtica i que té asimetria negativa o per l’esquerra.
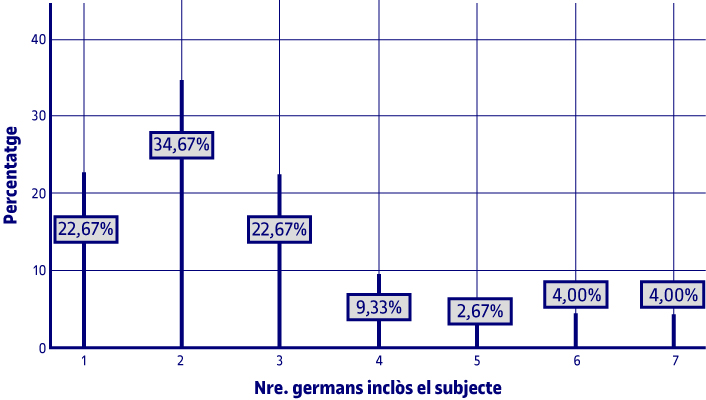
A la gràfica s’observa, per exemple, que el valor més repetit de nombre de germans, inclòs el subjecte, és 2, valor que coincideix amb el de la moda. Una altra dada que s’observa, per exemple, és que el 4 % té sis germans, inclòs ell, i aquest percentatge es repeteix per als que tenen set germans, inclosos ells.
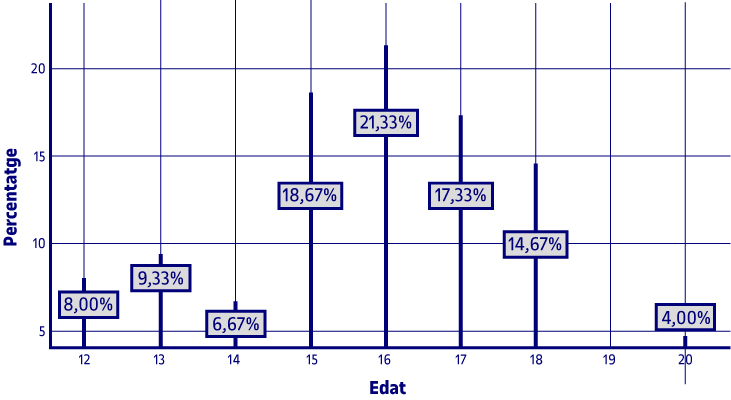
En la gràfica s’observa, per exemple, que el valor d’edat més repetit és 16, que coincideix amb el de la moda. Una altra dada que s’observa és que ningú no té 19 anys.
Encara que hi ha més variables relacionades entre elles, ens limitarem a estudiar les variables que estan relacionades de manera directa o inversa amb les xarxes socials més utilitzades per intentar establir un perfil per a cada tipus de xarxa. Si mirem la taula, veiem que per a un nivell de confiança del 99 % està relacionada amb els estudis que cursa i l’edat i, si considerem un nivell de confiança del 95 %, aquesta variable està relacionada amb els estudis que cursa, els estudis del pare i l’edat.
Així, doncs, a partir d’ara considerarem que el nivell de confiança és del 95 %.
Per als estudis que cursa i la xarxa social, veiem que el coeficient de correlació de Pearson és negatiu, i això vol dir que la relació és inversa, és a dir, que com més codificació de l’estudi cursat menys codificació pel que fa a la xarxa social, i el passa mateix entre les altres variables relacionades.
Com que veiem que està relacionada amb aquestes tres variables, demanarem la recta de regressió lineal considerant com a variable depenent la variable de xarxes socials i, com a independent, les tres assenyalades.
| Variables entrades/eliminadesa | |||
| Model | Variables entrades | Variables eliminades | Mètode |
| 1 | Edat, estudis del pare, estudis que cursab | . | Introduir |
Aquesta taula ens indica les variables que han entrat en el model, les quals són les identificades com a correlacionades amb la dependent.
| Resum del model | ||||
| Model | R | R quadrat | R quadrat ajustat | Error estàndard de l’estimació |
| 1 | ,490a | ,240 | ,208 | 1,956 |
Si mirem el resum del model, el coeficient de determinació (R quadrat) és el de correlació al quadrat, i val 0,240, la qual cosa significa que el 24 % de la variabilitat de la variable Xarxa social és representada per la recta de regressió.
| ANOVAa | ||||||
| Model | Suma de quadrats | gl | Mitjana quadràtica | F | Sig. | |
| 1 | Regressió | 85,753 | 3 | 28,584 | 7,471 | ,000b |
| Residu | 271,633 | 71 | 3,826 | |||
| Total | 357,387 | 74 | ||||
![]() No hi ha regressió
No hi ha regressió
![]()
![]() (hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
(hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
El contrast que fem és que no hi ha regressió. Com que p-valor val 0, el contrast és significatiu i, per tant, té sentit fer la recta de regressió.
| Coeficientsa | ||||||
| Model | Coeficients no estandarditzats | Coeficients estandarditzats | t | Sig. | ||
| B | Desv. Error | Beta | ||||
| 1 | (Constant) | 12,718 | 2,281 | 5,575 | ,000 | |
| Estudis que cursa | -,527 | ,402 | -,178 | -1,311 | ,194 | |
| Estudis del pare | -,958 | ,286 | -,357 | -3,351 | ,001 | |
| Edat | -,317 | ,153 | -,286 | -2,070 | ,042 | |
Ens queda escriure l’equació de la recta de regressió. Si mirem la taula, la recta de regressió és:
![]()
![]() Els coeficients són nuls
Els coeficients són nuls
![]()
![]() (hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
(hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
Com que els p-valors associats a la constant i els coeficients associats a les variables Estudis del pare i Edat són menors o iguals a 0,05, podem considerar que tant la constant com aquests dos coeficients són no nuls, cosa que no passa en el coeficient associat a la variable Estudis que cursa. Això vol dir que hem de demanar de nou la recta de regressió traient la variable Estudis que cursa per a un nivell de confiança del 95 %.
| Variables entrades/eliminadesa | |||
| Model | Variables entrades | Variables eliminades | Mètode |
| 1 | Edat, Estudis del pareb | . | Introduir |
Aquesta taula ens indica les variables que han entrat en el model, que són les identificades com a correlacionades amb la dependent i de coeficients no nuls.
| Resum del model | ||||
| Model | R | R quadrat | R quadrat ajustat | Error estàndard de l’estimació |
| 1 | ,471a | ,222 | ,200 | 1,966 |
Si mirem el resum del model, el coeficient de determinació (R quadrat) és el de correlació al quadrat i val 0,222, la qual cosa significa que el 22,2 % de la variabilitat de la variable Xarxa social està representada per la recta de regressió.
| ANOVAa | ||||||
| Model | Suma de quadrats | gl | Suma de quadrats | F | Sig. | |
| 1 | Regressió | 79,173 | 2 | 39,587 | 10,245 | ,000b |
| Residu | 278,213 | 72 | 3,864 | |||
| Total | 357,387 | 74 | ||||
![]() No hi ha regressió
No hi ha regressió
![]()
![]() (hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
(hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
El contrast que fem és que no hi ha regressió i, com que el p-valor val 0, és significatiu i, per tant, té sentit fer la recta de regressió.
| Coeficientsa | ||||||
| Modelo | Coeficients no estandarditzats | Coeficients estandarditzats | t | Sig. | ||
| B | Desv. Error | Beta | ||||
| 1 | (Constant) | 13,655 | 2,177 | 6,272 | ,000 | |
| Estudis del pare | -,958 | ,287 | -,357 | -3,334 | ,001 | |
| Edat | -,445 | ,118 | -,402 | -3,759 | ,000 | |
Ens queda escriure l’equació de la recta de regressió. Si mirem la taula, la recta de regressió és:
![]()
![]() Els coeficients són nuls
Els coeficients són nuls
![]()
![]() (hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
(hipòtesi alternativa), la qual cosa significa que es rebutja la hipòtesi nul·la.
Com que els p-valors de la constant i dels altres coeficients són menors o iguals a 0,05, podem considerar que tant la constant com aquests dos coeficients són no nuls per a un nivell de confiança del 95 %.

