7.7. Mesures descriptives
L’estadística descriptiva utilitza mesures per descriure el fenomen que s’estudia. Les mesures més utilitzades són:
a) La moda (Mo)
És el valor que es presenta amb major freqüència en una distribució. Pot haver-n’hi més de dues. Quan n’hi ha una, parlem de distribució «unimodal», i quan n’hi ha dues ens referim a «bimodals».
Un exemple és:
Grau d’acord entre els pares per promoure la lectura dels diaris impresos entre els adolescents de dotze a disset anys:
| Grau d’acord | Freqüències |
| Molt d’acord | 20 |
| Bastant d’acord | 60 |
| Indiferent | 10 |
| Poc d’acord | 8 |
| Molt en desacord | 2 |
| Total (N) | 100 |
En aquest cas, la moda és la categoria «bastant d’acord», triada per seixanta persones.
Si ens referim a dades agrupades, la moda serà el punt mitjà de l’interval en què estigui la moda. El punt mitjà s’obté sumant els dos extrems i dividint-los entre dos.
Un exemple és:
Exemple
Nombre d’hores setmanals que els estudiants de primer de Comunicació dediquen a xatejar amb WhatsApp:
| Hores setmanals | Freqüències |
| 0-1 | 18 |
| 2-3 | 10 |
| 4-5 | 12 |
| 6-7 | 40 |
| Total | 80 |
Mo: 6,5
En aquest cas la moda és 6,5. La xifra s’obté de sumar 6 i 7 i dividir-ho entre 2.
Exemple de variable quantitativa discreta
Calcula la moda de les dades següents: 1,1,2,3,3,3,5,7,7,8,9.
Solució
El valor de la variable que es repeteix més és 3; per tant, la moda és 3.
Si la variable és quantitativa contínua, la moda tampoc no ha de ser única.
Per a cada interval 
màxim s’aplica la fórmula següent:
Essent:
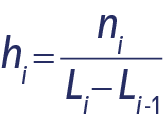
és l’extrem inferior de l’interval modal, 
l’extrem superior de l’interval anterior, n la grandària de la mostra, 
la freqüència absoluta corregida corresponent a l’interval modal, 
la freqüència absoluta corregida corresponent a l’interval anterior al modal, i 
la freqüència absoluta corregida corresponent a l’interval posterior a l’interval modal.
En el cas que tots els intervals tinguin la mateixa amplitud es verifica que 
.
Exemple de variable quantitativa contínua amb intervals de la mateixa amplitud
Calcula la moda de les dades següents:
 |
 |
| [1,2) | 15 |
| [2,3) | 25 |
| [3,4) | 10 |
Solució
Com que els intervals tenen la mateixa amplitud, no fa falta calcular . L’interval modal és el [2,3), perquè és el de més freqüència absoluta, i apliquem la fórmula per determinar el valor de la moda:
Exemple de variable quantitativa contínua amb intervals d’amplitud diferent
Calcula la moda de les dades següents:
|
|
| [1,2) | 15 |
| [2,4) | 25 |
| [4,7) | 10 |
Solució
Com que els intervals no tenen la mateixa amplitud, fa falta calcular .
|
|
|
| [1,2) | 15 | 15 |
| [2,4) | 25 |  |
| [4,7) | 10 |  |
Com que el màxim és 15, l’interval modal és el [1,2), i apliquem la fórmula per determinar el valor de la moda:
b) La mediana
És el punt o valor numèric que deixa la meitat de les puntuacions per sota. S’ordenen de més petit a més gran tots els casos i es troba el cas que estigui en el punt mitjà. Quan són distribucions imparelles, la mediana està en tot el centre. Es calcula de la manera següent:
Hores de consum de Facebook de cinc estudiants:
5 6 7 8 9
La mediana és 7, exactament al centre. Obtenim el mateix nombre si apliquem la fórmula.
Si la distribució és parella, per exemple, el nombre d’hores setmanals que sis amics veuen Netflix:
18 20 28 30 42 44
Les dades numèriques que deixen per sobre i per sota d’un nombre igual de dades són 28 i 30. Se sumen i es divideixen per 2:
Exemple de variable quantitativa discreta
Calcula la mediana de les dades següents: 1,1,2,3,3,3,5,7,7,8,9.
Solució
 |
|
 |
| 1 | 2 | 2 |
| 2 | 1 | 3 |
| 3 | 3 | 6 |
| 5 | 1 | 7 |
| 7 | 2 | 9 |
| 8 | 1 | 10 |
| 9 | 1 | 11 |
. Tal com veiem en la columna de les freqüències absolutes acumulades, en el valor 6 és on ens passem per primera vegada de 5,5; per tant, el valor de la mediana és 3.
D’una altra manera, ens quedem amb el que ocupa el lloc central després d’ordenar les dades.
1,1,2,3,3,3,5,7,7,8,9
Exemple
Calcula la mediana de les dades següents: 1,1, 2,3, 3,3, 5,7, 7,8, 9,9.
Solució
|
|
|
| 1 | 2 | 2 |
| 2 | 1 | 3 |
| 3 | 3 | 6 |
| 5 | 1 | 7 |
| 7 | 2 | 9 |
| 8 | 1 | 10 |
| 9 | 2 | 12 |
Els dos valors centrals, després d’ordenar les dades de la variable de més petita a més gran, són el 3 i el 5:
1,1, 2,3, 3,3, 5,7, 7,8, 9,9
D’una altra manera, ens fixem en quin valor de la variable té com a freqüència absoluta la meitat de les dades i calculem la mitjana d’aquest valor i del següent.
Si la variable és quantitativa contínua, la mediana estarà en aquell interval en la freqüència absoluta acumulada del qual passem de menys de la meitat a més de la meitat de les dades, ordenades prèviament de més petita a més gran. Si la freqüència absoluta acumulada coincideix amb la meitat de les dades, la mediana és l’extrem de l’interval, i en cas contrari s’aplica la fórmula següent:
essent 
l’extrem inferior de l’interval mitjà, l’extrem superior de l’interval anterior, n la grandària de la mostra, la freqüència absoluta acumulada que es passa del valor de la meitat de les dades, i finalment 
la freqüència absoluta acumulada anterior a la seleccionada.
Exemple de variable quantitativa contínua
Calcula la mediana de les dades següents:
|
|
| [1,2) | 15 |
| [2,3) | 25 |
| [3,4) | 10 |
Solució
|
|
|
| [1,2) | 15 | 15 |
| [2,3) | 25 | 40 |
| [3,4) | 10 | 50 |
Com que el nombre total de dades és 50, i la meitat d’aquestes són 25, l’interval mitjà seria [2,3), perquè la seva freqüència absoluta acumulada és de 40 (la primera freqüència absoluta acumulada que passa de 25).
Exemple
Calcula la mediana de les dades següents:
|
|
| [1,2) | 25 |
| [2,3) | 5 |
| [3,4) | 20 |
Solució
|
|
|
| [1,2) | 25 | 25 |
| [2,3) | 5 | 30 |
| [3,4) | 20 | 50 |
Com que el nombre total de dades és 50, i la meitat d’aquestes és 25, l’interval mitjà seria [1,2), perquè la seva freqüència absoluta acumulada és de 25 i el valor de la mediana coincideix en aquest cas amb l’extrem superior de l’interval, és a dir, 
.
c) La mitjana aritmètica i la mitjana ponderada
La mitjana aritmètica ens informa de la mesura de tendència central d’un grup de dades. S’obté quan se sumen tots els valors i es divideix pel total de casos.
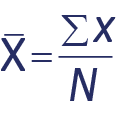
És la mitjana aritmètica.
Σ És el símbol de la lletra grega sigma en majúscules i fa referència a la suma.
x És cadascun dels valors observats.
N és el nombre total de puntuacions d’una distribució.
Per exemple, si volem obtenir la mitjana de les notes (6, 5 i 7) de tres treballs de l’assignatura Metodologies de la recerca d’un alumne:
Si l’última d’aquestes notes tingués tres vegades més valor que les altres, parlaríem de la mitjana ponderada i es calcularia així:
Exemple de mitjana aritmètica
Es van seleccionar cinc persones i se’ls va preguntar el nombre d’hores al dia que passaven connectats a qualsevol xarxa social. Les dades van ser les següents: 2,1; 5,3; 1,4; 4,6; 0,7. Calculeu la mitjana del temps en hores al dia que van passar connectats a les xarxes socials.
Solució
X ≡ temps en hores de connexió al dia a xarxes socials.
Es tracta d’una variable quantitativa contínua.
Exemple de mitjana ponderada
Amb les dades de l’apartat anterior, i tenint en compte que hem ponderat cada subjecte respectivament amb els valors 1, 2, 3, 4, i 5, s’han donat aquests valors en concordança amb les edats dels enquestats: com menys edat més pes. Calculeu la mitjana geomètrica del temps en hores al dia que van passar connectats a xarxes socials.
Solució
d) Percentils
És una mesura de posició no central que ens diu la posició d’un valor respecte als altres. Per exemple, si un valor està en el quartil 2 (Q2), ens diu que dues quartes parts de les dades són iguals o menors que aquest valor.
Si un valor té un percentil 20 (P20), el 20 % de les dades restants tindrà el seu mateix valor o menys.
Per exemple, estem estudiant les hores de consum diari d’Instagram de joves universitaris entre 18 i 22 anys. Si el consum de quatre hores està en el percentil 80 (P80), el 80 % d’aquests estudiants utilitza Instagram durant quatre hores o menys.
El percentil k és el primer valor de la variable que deixa inferiors o iguals a ell les 
parts de les observacions. Es calcula el valor i es tria l’interval la freqüència absoluta acumulada del qual és igual o major que aquest valor.
Hi ha cent percentils. Per definició, 
Exemple de variable quantitativa discreta
Calcula el percentil 1 de les dades següents: 1,1, 2,3, 3,3, 5,7,7,8,9.
Solució
|
|
|
| 1 | 2 | 2 |
| 2 | 1 | 3 |
| 3 | 3 | 6 |
| 5 | 1 | 7 |
| 7 | 2 | 9 |
| 8 | 1 | 10 |
| 9 | 1 | 11 |
El percentil 1 deixarà per sota seu la centèsima part de les observacions.
Calculem el percentil 1.
. Si ens fixem en la columna de les freqüències absolutes acumulades, la primera que passa d’aquest valor és 2, que es correspon amb el valor de la variable 1; per tant: 
Exemple de variable quantitativa contínua
Calcula el percentil 97 tenint en compte les dades següents:
|
|
|
| [1,2) | 15 | 15 |
| [2,3) | 25 | 40 |
| [3,4) | 10 | 50 |
Solució
El percentil 97 deixarà el 97 % de les observacions per sota seu.
En aquest cas particular, com que hi ha cinquanta dades, deixarà per sota:
Si ens fixem en la columna de les freqüències absolutes acumulades, la primera que passa d’aquest valor és 50; per tant, ens quedem amb l’interval [3,4) i apliquem la fórmula.
