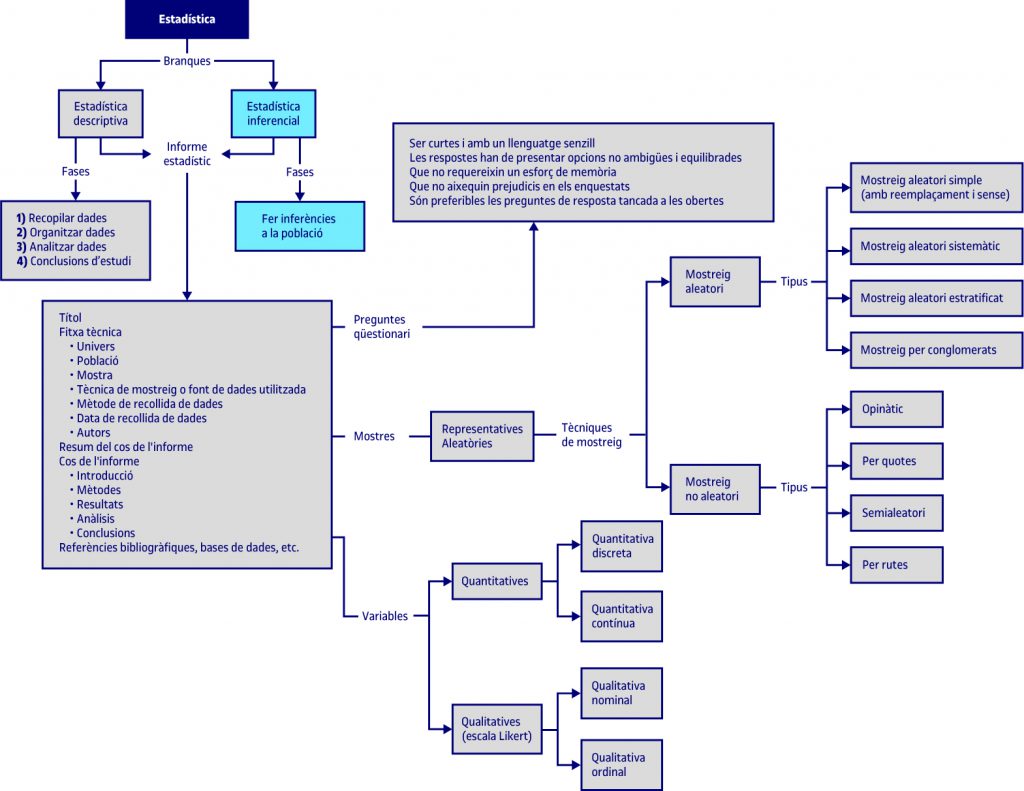
8.3. Tècniques de mostreig
8.3.7. Mostrejos no aleatoris
En aquest tipus de mostreig es té en compte el criteri de l’investigador. Això vol dir que la representativitat no està garantida. Com indica Vinuesa (ibíd., pàg. 189), amb aquest tipus de mostreig els components de l’univers no tenen les mateixes possibilitats de formar part de l’estudi. L’error pot ser major amb aquest tipus de mostrejos.
Mostreig opinàtic
Es pregunta a qui es vol.
Mostreig per quotes
Quan l’estratificació no és possible o resulta molt cara, i també en casos en què no es disposa d’una llista de la població a investigar, es pot recórrer a l’anomenat mostreig per quotes. És un dels més utilitzats gràcies a la seva facilitat i rapidesa. En la primera fase és un mostreig opinàtic i es fixen límits per diversificar la mostra.
No obstant això, com s’ha assenyalat, la fiabilitat presenta problemes, com per exemple que s’acudeixi a persones properes per aplicar les tècniques de recol·lecció d’informació i això imposi un biaix en la recerca.
Mostreig semialeatori
És la mescla d’un d’aleatori amb un de no aleatori.
Mostreig per rutes
És gairebé aleatori. Consisteix a preguntar amb un plànol amb unes lleis de moviment.
Hem de rebutjar aquest tipus de mostrejos. Perquè es consideri vàlida una mostra, i per tant l’estudi estadístic entorn d’ella, ha de complir les condicions següents:
- Ser representativa
Aquesta condició està associada a la grandària de la mostra. És evident que, com més gran sigui la grandària de la mostra, més s’aproximarà a la grandària de la població i, per tant, més representativa serà. Però en la majoria dels estudis no és òptim estudiar tota la població, ni grandàries de mostra molt grans, i per això es recorren a les tècniques de mostreig.
- Ser aleatòria
És a dir, qualsevol element de la població pot ser triat per formar part de la mostra perquè tots tenen la mateixa probabilitat quant a elecció; no hi ha uns elements més probables que uns altres. En cas contrari, correm el risc de triar elements per a la mostra que compleix una determinada condició, amb la qual cosa estaríem falsejant els resultats estadístics i l’estudi seria declarat no vàlid. En el cas que la mostra no sigui aleatòria, es diu que s’han comès errors de biaix.
Resumint a manera d’esquema: