7.7. Medidas descriptivas
La estadística descriptiva utiliza las medidas para describir el fenómeno que se está estudiando. Las medidas más utilizadas son:
a. La Moda (Mo)
Es el valor que se presenta con mayor frecuencia en una distribución. Puede haber más de dos. Cuando hay una hablamos de distribución «unimodal» y cuando hay dos, nos referimos a «bimodales».
En el siguiente ejemplo:
Grado de acuerdo entre los padres para promover la lectura de los diarios impresos entre los adolescentes de 12-17 años:
| Grado de acuerdo | Frecuencias |
| Muy de acuerdo | 20 |
| Bastante de acuerdo | 60 |
| Indiferente | 10 |
| Poco de acuerdo | 8 |
| Muy en desacuerdo | 2 |
| Total (N) | 100 |
La moda, en este caso, es la categoría «Bastante de acuerdo» elegida por sesenta personas.
Si nos referimos a datos agrupados, la moda será el punto medio del intervalo en que se encuentre la moda. El punto medio se obtiene sumando los dos extremos y dividiéndolos entre dos.
Como en este ejemplo:
Número de horas semanales que los estudiantes de primero de Comunicación dedican a chatear en WhatsApp
| Horas semanales | Frecuencias |
| 0-1 | 18 |
| 2-3 | 10 |
| 4-5 | 12 |
| 6-7 | 40 |
| Total | 80 |
Mo: 6,5
En este caso, la moda es 6,5. La cifra sale de sumar 6 y 7 y dividirlo entre 2.
Ejemplo variable cuantitativa discreta:
Calcula la moda de los siguientes datos: 1,1,2,3,3,3,5,7,7,8,9
Solución:
El valor de la variable que más se repite es 3, por tanto, la moda es 3.
Si la variable es cuantitativa continua tampoco tiene que ser única la moda en este caso.
Para cada intervalo 
máximo se aplica la siguiente fórmula:
Siendo:
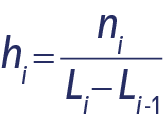
es el extremo inferior del intervalo modal, 
el extremo superior del intervalo anterior, n el tamaño de la muestra, 
la frecuencia absoluta corregida correspondiente del intervalo modal, 
la frecuencia absoluta corregida correspondiente al intervalo anterior al modal y 
la frecuencia absoluta corregida correspondiente al intervalo posterior al intervalo modal.
En el caso de que todos los intervalos tengan la misma amplitud, se verifica que 
Ejemplo variable cuantitativa continua, con intervalos de la misma amplitud:
Calcula la moda de los siguientes datos:
 |
 |
| [1,2) | 15 |
| [2,3) | 25 |
| [3,4) | 10 |
Solución:
Como los intervalos tienen la misma amplitud no hace falta calcular . El intervalo modal es el [2,3), porque es el de mayor frecuencia absoluta, aplicamos la fórmula, para determinar el valor de la moda:
Ejemplo variable cuantitativa continua, con intervalos de diferente amplitud:
Calcula la moda de los siguientes datos:
|
|
| [1,2) | 15 |
| [2,4) | 25 |
| [4,7) | 10 |
Solución:
Como los intervalos no tienen la misma amplitud, hace falta calcular .
|
|
|
| [1,2) | 15 | 15 |
| [2,4) | 25 |  |
| [4,7) | 10 |  |
Como el máximo es 15, el intervalo modal es el [1,2), aplicamos la fórmula, para determinar el valor de la moda:
b. La mediana
Es el punto o valor numérico que deja por debajo a la mitad de las puntuaciones. Se ordenan de menor a mayor todos los casos y se halla el caso que esté en el punto medio. Cuando son distribuciones impares, la mediana está en todo el centro. Se calcula de la siguiente manera:
Ejemplo: Horas de consumo de Facebook de cinco estudiantes:
5 6 7 8 9
La mediana es 7, exactamente en el centro. Exactamente el mismo número si aplicamos la fórmula.
Si la distribución es par. Por ejemplo, número de horas semanales que seis amigos ven Netflix:
18 20 28 30 42 44
Los datos numéricos que dejan por encima y por debajo a un número igual de datos son 28 y 30. Se suman y se dividen por 2:
Ejemplo variable cuantitativa discreta:
Calcula la mediana de los siguientes datos:1,1,2,3,3,3,5,7,7,8,9
Solución:
 |
|
 |
| 1 | 2 | 2 |
| 2 | 1 | 3 |
| 3 | 3 | 6 |
| 5 | 1 | 7 |
| 7 | 2 | 9 |
| 8 | 1 | 10 |
| 9 | 1 | 11 |
; por tanto, mirando en la columna de las frecuencias absolutas acumuladas, en el valor 6 es dónde nos pasamos por primera vez de 5,5; por tanto, el valor de la mediana es 3.
De otra manera: te quedas con el que ocupa el lugar central previamente ordenado los datos.
1,1,2,3,3,3,5,7,7,8,9
Ejemplo:
Calcula la mediana de los siguientes datos: 1,1, 2,3, 3,3, 5,7, 7,8, 9,9
Solución:
|
|
|
| 1 | 2 | 2 |
| 2 | 1 | 3 |
| 3 | 3 | 6 |
| 5 | 1 | 7 |
| 7 | 2 | 9 |
| 8 | 1 | 10 |
| 9 | 2 | 12 |
Los dos valores centrales, previamente ordenados los datos de la variable de menor a mayor son el 3 y el 5:
1,1, 2,3, 3,3, 5,7, 7,8, 9,9
De otra forma, nos fijamos en qué valor de la variable tiene de frecuencia absoluta la mitad de los datos y calculamos la media de ese valor y del siguiente.
Si la variable es cuantitativa continua:
La mediana estará en aquel intervalo en cuya frecuencia absoluta acumulada, pasamos de menos de la mitad a más de la mitad de los datos, previamente ordenados de menor a mayor. Si resulta que la frecuencia absoluta acumulada coincide con la mitad de los datos, entonces la mediana sería el extremo del intervalo, en caso contrario se aplica la siguiente fórmula:
siendo 
el extremo inferior del intervalo mediano el extremos superior del intervalo anterior, n el tamaño de la muestra, la frecuencia absoluta acumulada que se pasa del valor de la mitad de los datos y por último 
la frecuencia absoluta acumulada anterior a la seleccionada.
Ejemplo variable cuantitativa continua:
Calcula la mediana de los siguientes datos:
|
|
| [1,2) | 15 |
| [2,3) | 25 |
| [3,4) | 10 |
Solución:
|
|
|
| [1,2) | 15 | 15 |
| [2,3) | 25 | 40 |
| [3,4) | 10 | 50 |
Como el número total de datos es 50, y la mitad de esto 25, el intervalo mediano sería [2,3); porque su frecuencia absoluta acumulada es de 40 (la primera frecuencia absoluta acumulada que se pasa de 25).
Ejemplo:
Calcula la mediana de los siguientes datos:
|
|
| [1,2) | 25 |
| [2,3) | 5 |
| [3,4) | 20 |
Solución:
|
|
|
| [1,2) | 25 | 25 |
| [2,3) | 5 | 30 |
| [3,4) | 20 | 50 |
Como el número total de datos es 50, y la mitad de esto 25, el intervalo mediano sería [1,2); porque su frecuencia absoluta acumulada es de 25 y el valor de la mediana coincide en este caso con el extremo superior del intervalo, es decir, 
c. La media aritmética y la media ponderada
Es el mismo «promedio aritmético», nos informa sobre la medida de tendencia central de un grupo de datos. Se obtiene cuando se suman todos los valores y se divide por el total de casos.
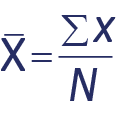
Es la media aritmética.
Σ Es el símbolo de la letra griega sigma en mayúscula y hace referencia a la suma.
x Es cada uno de los valores observados.
N es el número total de puntuaciones de una distribución.
Por ejemplo, si queremos sacar las notas de un alumno de Metodologías de la investigación en tres trabajos: 6, 5 y 7, la media sería:
Si la última de esas notas tuviera 3 veces más valor que las demás, hablaríamos de la media ponderada y se calcularía así:
Ejemplo media aritmética:
Se seleccionaron cinco personas y se les preguntó el número de horas al día que pasaban conectados a cualquier red social. Los datos fueron los siguientes: 2,1; 5,3; 1,4; 4,6; 0,7. Calculad: La media del tiempo de horas/día que pasaron conectados a redes sociales.
Solución:
X ≡ tiempo de horas conexión al día a redes sociales.
Se trata de una variable cuantitativa continua.
Ejemplo de media ponderada:
Con los datos del apartado anterior y teniendo en cuenta que hemos ponderado a cada sujeto respectivamente con los valores 1, 2, 3, 4, y 5, estos valores se han dado acordes a las edades de los encuestados, a menos edad mayor peso. Calculad: La media geométrica del tiempo de horas/día que pasaron conectados a redes sociales.
Solución:
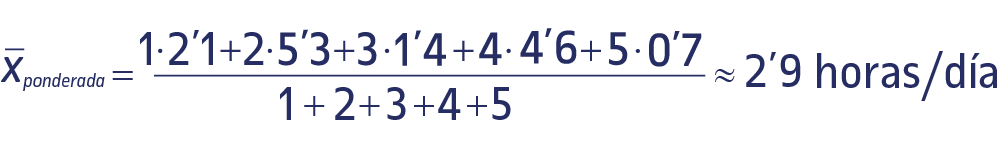
d. Percentiles
Es una medida de posición no central que nos dice la posición de un valor respecto a los demás. Por ejemplo, si un valor está en el cuartil 2 (Q2), nos dice que dos cuartas partes de los datos son iguales o menores a ese valor.
Si un valor tiene un percentil 20 (P20), el 20 % de los datos restantes tendrá su mismo valor o menos.
Por ejemplo, estamos estudiando las horas de consumo diario de Instagram de jóvenes universitarios entre 18 y 22 años. Si el consumo de 4 horas se encuentra en el percentil 80 (P80) nos indica que el 80 % de esos estudiantes utiliza Instagram durante 4 horas o menos.
El percentil k es el primer valor de la variable que deja inferiores o iguales a él, las 
partes de las observaciones. Se calcula el valor y se elige aquel intervalo cuya frecuencia absoluta acumulada es igual o mayor de ese valor.
Hay 100 percentiles. Por definición 
Ejemplo variable cuantitativa discreta:
Calcula el percentil 1 de los siguientes datos: 1,1, 2,3, 3,3, 5,7,7,8,9
Solución:
|
|
|
| 1 | 2 | 2 |
| 2 | 1 | 3 |
| 3 | 3 | 6 |
| 5 | 1 | 7 |
| 7 | 2 | 9 |
| 8 | 1 | 10 |
| 9 | 1 | 11 |
El percentil 1 dejará por debajo de él la centésima parte de las observaciones.
Vamos a calcular el percentil 1.
si nos fijamos en la columna de las frecuencias absolutas acumuladas, la primera que pasa de ese valor es el 2, que se corresponde con el valor de la variable 1, por tanto: 
Ejemplo variable cuantitativa continua:
Calcula el percentil 97, teniendo en cuenta los siguientes datos:
|
|
|
| [1,2) | 15 | 15 |
| [2,3) | 25 | 40 |
| [3,4) | 10 | 50 |
Solución:
El percentil 97, dejará el 97 % de las observaciones por debajo de él.
En este caso particular, como hay 50 datos, dejaría por debajo:
Si nos fijamos en la columna de las frecuencias absolutas acumuladas, la primera que pasa de ese valor es 50, por lo tanto, nos quedamos con el intervalo [3,4) y aplicamos la fórmula.
